Swift Leetcode 栈、队列算法题解

1.最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。

示例:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]


输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

pop、top 和 getMin 操作总是在非空栈上调用。

class MinStack {

    var head:ListNode?
    
    init() {
        head = ListNode(min:Int.max)
    }
    
    func push(_ val: Int) {
        //每次push都记录最小值
        head = ListNode(val: val, min: min(val, head!.min), next: head)
    }
    
    func pop() {
        head = head?.next
    }
    
    func top() -> Int {
        return head?.val ?? 0
    }
    
    func getMin() -> Int {
        return head?.min ?? 0
    }

    class ListNode {
        let val: Int
        let min:Int
        let next: ListNode?

        init(val: Int = 0,min:Int = 0,next:ListNode? = nil) {
             self.val = val
             self.min = min
             self.next = next
        }
        
    }

}


/**
 * Your MinStack object will be instantiated and called as such:
 * let obj = MinStack()
 * obj.push(val)
 * obj.pop()
 * let ret_3: Int = obj.top()
 * let ret_4: Int = obj.getMin()
 */

解题思路：

题目要求我们从栈元素中找到最小值，按照正常想，我们都会遍历一遍栈的元素，但是这样时间复杂度就是O(n),题目要求是O(1)，一般遇到这种问题，就需要空间换时间了。
使用链表，在每个节点保存当前的最小值，每次push都记录当前元素对应的最小值，每个节点都一一对应一个最小值，这样子getMin时间复杂度就是O(1)，同道理，这里用两个栈也可以做到一一对应也能解决。

2.滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

提示

1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length

class Solution {
    
    struct Deque<T> {
        private var array = [T]()
        //判空
        var isEmpty: Bool {
            return array.isEmpty
        }
        var count: Int {
            return array.count
        }
        //从队尾入队
        mutating func enqueue(_ element: T) {
            array.append(element)
        }
        //从队首入队
        mutating func enqueueInsert(_ element: T) {
            array.insert(element, at: 0)
        }
        //从队首出队
        mutating func removeFirst() -> T? {
            if isEmpty {
                return nil
            } else {
                return array.removeFirst()
            }
        }
        //从队尾出队
        mutating func removeLast() -> T? {
            if isEmpty {
                return nil
            } else {
                return array.removeLast()
            }
        }
        //查看队首元素
        func getFirst() -> T? {
            return array.first
        }
        //查看队尾元素
        func getLast() -> T? {
            return array.last
        }
    }
    
    func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
        if nums.count == 0 || k < 1 { return [Int]()}
        if k == 1 { return nums }
        
        var maxes = [Int](repeating: 0, count: nums.count - k + 1)
        
        var deque = Deque<Int>()
        for ri in 0..<nums.count {
            // 从队尾开始遍历只要nums[队尾] <= nums[ri]，就删除队尾
            while !deque.isEmpty && nums[deque.getLast() ?? 0] <= nums[ri]  {
                _ = deque.removeLast()
            }
            
            // 将ri加到队尾
            deque.enqueue(ri)
            
            // 检查窗口的索引是否合法
            let li = ri - k + 1
            if li < 0 {
                continue
            }
            
            // 检查队首的合法性
            let temp = deque.getFirst() ?? 0
            if temp < li {
                // 队首不合法（失效，不在滑动窗口索引范围内）
                _ = deque.removeFirst()
            }
            
            // 设置窗口的最大值
            maxes[li] = nums[deque.getFirst() ?? 0]
            
        }
        
        return maxes
    }
    
}

解题思路：

使用到双端队列的特性，队首队尾均可进出的特性，实现单调队列
单调队列从队首到队尾，nums[队列元素]，是逐渐减小的
队列里存放的是对应值的索引
每次入队列都需要从队尾开始遍历只要nums[队尾] <= nums[ri]，就删除队尾(比较是否大于队尾，大于就删除)
每次移动窗口都需要检查队首的合法性（失效，不在滑动窗口索引范围内）就需要删除队首元素
最后取出单调队列的队首设置最大值（也就是窗口的最大值）

3.最大二叉树

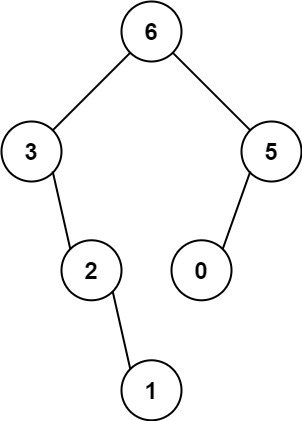
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的最大二叉树定义如下：

二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中最大值左边部分递归构造出的最大二叉树。
右子树是通过数组中最大值右边部分递归构造出的最大二叉树。
返回有给定数组 nums 构建的最大二叉树。

示例

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

提示

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public var val: Int
 *     public var left: TreeNode?
 *     public var right: TreeNode?
 *     public init() { self.val = 0; self.left = nil; self.right = nil; }
 *     public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }
 *     public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {
 *         self.val = val
 *         self.left = left
 *         self.right = right
 *     }
 * }
 */
class Solution {
    func constructMaximumBinaryTree(_ nums: [Int]) -> TreeNode? {
            guard nums.count != 0 else {return nil}
            return findRoot(nums,0,nums.count)
    }

    //查找[l, r)范围的根节点
    func findRoot(_ nums: [Int],_ l:Int,_ r:Int) -> TreeNode? {
            guard l != r else {return nil}

            // 遍历找出[l, r)范围内最大值的索引
            var maxIdx = l
      			//(l + 1)从第二个数开始比较, ..<r不包括r ...r包括r
            for i in (l + 1)..<r {
                if nums[i] > nums[maxIdx] {
                    maxIdx = i
                }
            }

            let treeNode = TreeNode(nums[maxIdx])
            //递归查找左子树
            treeNode.left = findRoot(nums,l,maxIdx)
            //递归查找右子树
            treeNode.right = findRoot(nums,maxIdx + 1,r)
            return treeNode

    }
}

解题思路：

这里需要每次都从数组分出最大子树根节点，以最大数字左边和右边一直对半找出最大数也就是最大根节点，一直细分到左右索引相等，所以这里可以用到递归的思路，递归调用找出最大根节点，注意这里是[l, r),[包括l )不包括r。

4.每日温度

请根据每日 气温 列表 temperatures ，请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

提示：
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100

func dailyTemperatures(_ temperatures: [Int]) -> [Int] {
        guard temperatures.count != 0 else {return []}
        var result = [Int](repeating: 0, count: temperatures.count)
        
        //新建一个单调递减的栈结构
        let stack = Stack<Int>()
        //遍历数组时间复杂度On
        for i in 0..<temperatures.count {
            //操作栈时间复杂度O1
            //每次入栈都需要判断栈顶是否大于需要入栈的元素，如果大于代表准备入栈的元素是出栈元素靠近右边第一个比它大的数值
            while !stack.isEmpty && temperatures[i] > temperatures[stack.top()] {
                //这里我们是记录相差的索引值 由于是左边遍历过去 i - stack.top()
                result[stack.top()] = i - stack.top()
                _ = stack.pop() //出栈
            }
            stack.push(i)
        }

        return result
    }


    class Stack<E>{
        var array = [E]()
        
        var isEmpty: Bool {
            return array.isEmpty
        }
        
        //入栈
        func push(_ element: E){
            array.append(element)
        }
        
        //移除栈顶元素
        func pop() -> E {
            array.removeLast()
        }
        
        //查看栈顶元素
        func top() -> E{
            array.last!
        }
        
        func size() -> Int {
            array.count
        }
    }

解题思路：

利用栈结构，实现一个单调递减栈，栈底放最大数，栈顶放最小数
遍历数组，每次跟栈顶的元素比较，如果小于栈顶元素直接入栈
如果大于代表准备入栈的元素是出栈元素（不符合单调递减栈规则，元素需要出栈）靠近右边第一个比它大的数值
计算索引差值，求出更高温度隔了几天

5.有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

输入：s = “()”
输出：true
示例 2：

输入：s = “()[]{}”
输出：true
示例 3：

输入：s = “(]”
输出：false
示例 4：

输入：s = “([)]”
输出：false
示例 5：

输入：s = “{[]}”
输出：true

提示：

1 <= s.length <= 104
s 仅由括号 ‘()[]{}’ 组成

class Solution {
    func isValid(_ s: String) -> Bool {
        //偶数直接返回false
        guard s.count%2 == 0 else {
            return false
        }
        // 哈希表存储左右对应的括号
        let map:[Character:Character] = [ 
                    "(":")",
                    "[":"]",
                    "{":"}"
        ]
        var stack = [Character]()
        for char in s {
            //包含规则(左括号类型)直接入栈
            if map.keys.contains(char) {
                stack.append(char)
            }else {
                //执行这里的代表是右括号类型，右括号类型与栈顶括号匹配,查看是否成功
                if stack.isEmpty  {//栈为空，返回false
                    return false
                }else if map[stack.last!] != char{//右括号类型与栈顶元素不匹配，返回false
                    return false
                }else {//右括号与栈顶匹配，出栈，继续遍历
                    stack.popLast()
                }
            }
        }
        //栈为空代表括号匹配都成功了，不为空就为不匹配
        return stack.isEmpty
    }
}

解题思路：

根据题目意思，我们能发现规律，先出现的左括号类型后匹配，所以我们能想到用栈的数据结构先进后出
新建一个map来存储左右括号的规则，遍历字符串，如果等于map的Key代表是左括号，直接入栈
如果不是代表是右括号类型，开始跟栈顶匹配，匹配就出栈继续遍历，不匹配直接返回false
栈为空代表括号匹配都成功了，不为空就为不匹配
字符串如果不是偶数是奇数直接返回，因为括号必须是成双成对的

6.用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

进阶：

你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

示例：

输入：
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

提示：

1 <= x <= 9
最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的（例如，一个空的队列不会调用 pop 或者 peek 操作）

class MyQueue {

    var s1 = [Int]() //负责入队元素的栈
    var s2 = [Int]() //负责出队元素的栈
    
    init() {

    }
    
    func push(_ x: Int) {
        s1.append(x)
    }
    
    func pop() -> Int {
        handleData()
        return s2.popLast() ?? 0
    }
    
    func peek() -> Int {
        handleData()
        return s2.last ?? 0
    }
    
    func empty() -> Bool {
        return s1.isEmpty && s2.isEmpty
    }

    //只要s2为空就需要遍历把s1元素依次添加进s2，s2栈顶元素一直是第一个入队的元素
    func handleData(){
        if s2.isEmpty {
            while !s1.isEmpty { //s1元素都popLast到s2直到为空
                s2.append(s1.popLast() ?? 0)
            }
        }
    }
}

解题思路：

这里使用双栈，s1负责入队元素的栈， s2负责出队元素的栈
s2栈顶时刻保持是第一个入队列的元素
pop()和peek()都需要判断s2是否为空，为空就需要遍历把s1元素依次添加进s2